第五章 自上而下的语法分析

自上而下

从文法的开始符号出发，反复使用各种产生式，寻找”匹配”的推导；
推导：根据文法的产生式规则，把串中出现的产生式的左部符号替换成右部；
针对输入串，试图用一切可能的办法，从文法开始符号(根结点)出发，自上而下地为输入串建立一棵语法树；
递归下降分析法、预测分析程序。

第一部分：LL(1)文法

1 多个产生式候选带来的问题

回溯问题：分析过程中，当一个非终结符用某一个候选匹配成功时，这种匹配可能是暂时的，出错时，不得不“回溯”；
文法左递归问题：左递归的文法可能由于语法错误导致陷入死循环。

2 直接左递归的消除

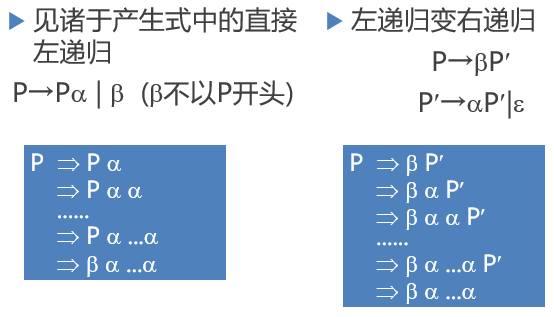
直接左递归的消除

直接左递归的消除

公式：
P→Pα1 | Pα2 |……| Pαm |β1 |β2 |……|βn
推导为：
P→β1P’|β2P’|…|βnP’
P’→α1P’|α2P’|…|αmP’|ε

例子：
给定文法G(E):
E→E＋T | T
T→TF | F
F→(E) | i
推导为：
G(E):
E→TE’
E’→+TE’ | ε
T→FT’
T’→FT’ | ε
F→(E) | i

3 间接左递归的消除

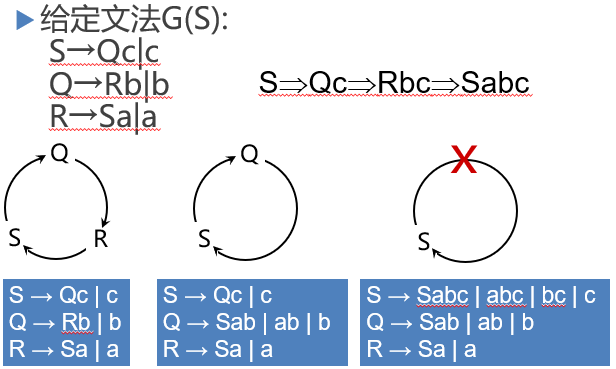
间接左递归的消除

间接左递归的消除

4 消除回溯

为了消除回溯必须保证对文法的任何非终结符，当要它去匹配输入串时，能够根据它所面临的输入符号准确地指派它的一个候选去执行任务，并且此候选的工作结果应是确信无疑的。

5 𝐹𝐼𝑅𝑆𝑇集合

令G是一个不含左递归的文法，对G的所有非终结符的每个候选𝛼定义它的终结首符集FIRST(𝛼)为：
𝐹𝐼𝑅𝑆𝑇(𝛼)={𝑎│𝛼∗⇒ 𝑎…, 𝑎∈𝑉𝑇}
特别是，若𝛼∗⇒ 𝜀，则规定𝜀∈𝐹𝐼𝑅𝑆𝑇(𝛼)。

6 𝐹𝑂𝐿𝐿𝑂𝑊集合

假定S是文法G的开始符号，对于G的任何非终结符A，我们定义A的FOLLOW集合：
𝐹𝑂𝐿𝐿𝑂𝑊(𝐴)={𝑎│𝑆∗⇒…𝐴𝑎…, 𝑎∈𝑉𝑇 }
特别是，若𝑆∗⇒…𝐴，则规定#∈𝐹𝑂𝐿𝐿𝑂𝑊(𝐴)

7 LL(1)文法

特点：

  1. 文法不含左递归
  2. 对于文法中每一个非终结符A的各个产生式的候选首符集两两不相交。
  3. 对文法中的每个非终结符A，若它存在某个候选首符集包含𝜀，则
    FIRST(𝛼i)∩FOLLOW(A)=#，i=1,2,…,n

对于LL(1)文法，可以对其输入串进行有效的无回溯的自上而下分析。
假设要用非终结符A进行匹配，面临的输入符号为a：

  1. 若a∈FIRST(𝛼i)，则指派𝛼i执行匹配任务；
  2. 若a不属于任何一个候选首符集，则：
    (1) 若𝛼属于某个FIRST(𝛼i)且 a∈FOLLOW(A)，则让A与𝛼自动匹配。
    (2) 否则，a的出现是一种语法错误。

第二部分：递归下降分析程序

8 递归下降分析器

分析程序由一组子程序组成， 对每一语法单位(非终结符)构造一个相应的子程序，识别对应的语法单位；
通过子程序间的相互调用实现对输入串的识别；
例如，A → B c D；
文法的定义通常是递归的，通常具有递归结构。

每个非终结符有对应的子程序的定义，在分析过程中，当需要从某个非终结符出发进行展开(推导)时，就调用这个非终结符对应的子程序。

例子：
定义全局过程和变量：
ADVANCE，把输入串指示器IP指向下一个输入符号，即读入一个单词符号；
SYM，IP当前所指的输入符号；
ERROR，出错处理子程序。
A→TE’ | BC | 𝜀 对应的递归下降子程序为： 

1
2
3
4
5
6
7
8
9
PROCEDURE  A；
BEGIN
  IF  SYM ∈FIRST(TE') THEN
    BEGIN  T；E' END
  ELSE IF  SYM ∈FIRST(BC) THEN
    BEGIN  B; C  END
  ELSE IF  SYM ∈FOLLOW(A) THEN
    ERROR
END；

9 扩充的巴科斯范式

在元符号“→”或“::=”和“|”的基础上，扩充几个元语言符号：
用花括号{α}表示闭包运算α*。
用表示{α}0n可任意重复0次至n次。
用方括号[α]表示{α}01，即表示α的出现可有可无(等价于α|𝜀)。

例如实数可定义为：
Decimal→[Sign]Integer.{digit}[Exponent]
Exponent→E[Sign]Integer
Integer→digit{digit}
Sign→ + | -

用扩充的巴科斯范式来描述语法，直观易懂，便于表示左递归消去和因子提取。

第二部分：预测分析程序

10 预测分析程序构成

总控程序，根据现行栈顶符号和当前输入符号，执行动作；
分析表 M[A，a]矩阵，A ∈ VN ，a ∈ VT 是终结符或‘＃’；
分析栈 STACK 用于存放文法符号。

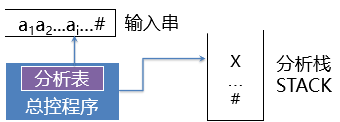
预测分析程序构成

预测分析程序构成

11 预测分析过程

总控程序根据当前栈顶符号X和输入符号a，执行下列三动作之一：

  1. 若X＝a＝‘＃’，则宣布分析成功，停止分析。
  2. 若X＝a ≠‘＃’，则把X从STACK栈顶逐出，让a指向下一个输入符号。
  3. 若X是一个非终结符，则查看分析表M。
    若M[X，a]中存放着关于X的一个产生式，把X逐出STACK栈顶，把产生式的右部符号串按反序一一推进STACK栈(若右部符号为𝜀，则意味不推什么东西进栈)。
    若M[X，a]中存放着“出错标志”，则调用出错诊察程序ERROR。

12 总控程序实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
BEGIN
  首先把‘＃’然后把文法开始符号推进STACK栈；
  把第一个输入符号读进a；
  FLAG:=TRUE;
  WHILE  FLAG  DO
  BEGIN
    把STACK栈顶符号上托出去并放在X中；
    IF X属于VT THEN
      IF X= a  THEN 把下一输入符号读进a
        ELSE   ERROR
      ELSE IF X=‘#’ THEN
        IF X=a THEN FLAG:=FALSE 
          ELSE ERROR
      ELSE IF M[X,a]={X→X1X2…Xk}THEN
      把Xk,Xk-1,…,X1一一推进STACK栈
      /* 若X1X2…Xk=𝜀，不推什么进栈 */
      ELSE ERROR
    END OF WHILE;
  STOP /*分析成功，过程完毕*/
END

13 预测分析示例

预测分析示例

预测分析示例

13 分析表M[A，a]的构造算法

构造G的分析表M[A，a]， 确定每个产生式A→α在表中的位置

  1. 对文法G的每个产生式A→α执行第2步和第3步；
  2. 对每个终结符a ∈ FIRST(α)，把A→α加至M[A，a]中；
  3. 若𝜀 ∈ FIRST(α)，则对任何b ∈ FOLLOW(A)把A→α加至M[A，b]中；
  4. 把所有无定义的M[A，a]标上“出错标志”。

14 LL(1)文法与二义性

如果G是左递归或二义的，那么，M至少含有一个多重定义入口。因此，消除左递归和提取左因子将有助于获得无多重定义的分析表M。
可以证明，一个文法G的预测分析表M不含多重定义入口，当且仅当该文法为LL(1)的。
LL(1)文法不是二义的。