并查集

用于解决连接问题
并查集

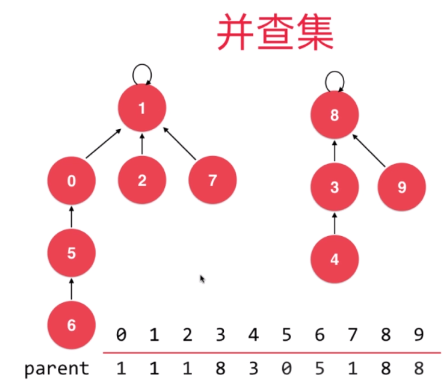
1 树结构并查集

初始条件下所有结点都为根节点，根节点指向自己。连接时，将一节点的根节点指向另一节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <cassert>

using namespace std;

namespace UF2{

    class UnionFind{

    private:
        // 使用一个数组构建一棵指向父节点的树
        // parent[i]表示第一个元素所指向的父节点
        int* parent;
        int count;  // 数据个数

    public:
        // 构造函数
        UnionFind(int count){
            parent = new int[count];
            this->count = count;
            // 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
            for( int i = 0 ; i < count ; i ++ )
                parent[i] = i;
        }

        // 析构函数
        ~UnionFind(){
            delete[] parent;
        }

        // 查找过程, 查找元素p所对应的集合编号
        int find(int p){
            assert( p >= 0 && p < count );
            // 不断去查询自己的父亲节点, 直到到达根节点
            // 根节点的特点: parent[p] == p
            while( p != parent[p] )
                p = parent[p];
            return p;
        }

        // 查看元素p和元素q是否所属一个集合
        // O(h)复杂度, h为树的高度
        bool isConnected( int p , int q ){
            return find(p) == find(q);
        }

        // 合并元素p和元素q所属的集合
        // O(h)复杂度, h为树的高度
        void unionElements(int p, int q){

            int pRoot = find(p);
            int qRoot = find(q);

            if( pRoot == qRoot )
                return;

            parent[pRoot] = qRoot;
        }
    };
}

2 树结构层数优化并查集

合并时将层数较少的集合指向层数较多的集合，减少树的总层数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <cassert>

using namespace std;

namespace UF4{

    class UnionFind{

    private:
        int* rank;   // rank[i]表示以i为根的集合所表示的树的层数
        int* parent; // parent[i]表示第i个元素所指向的父节点
        int count;   // 数据个数

    public:
        // 构造函数
        UnionFind(int count){
            parent = new int[count];
            rank = new int[count];
            this->count = count;
            for( int i = 0 ; i < count ; i ++ ){
                parent[i] = i;
                rank[i] = 1;
            }
        }

        // 析构函数
        ~UnionFind(){
            delete[] parent;
            delete[] rank;
        }

        // 查找过程, 查找元素p所对应的集合编号
        // O(h)复杂度, h为树的高度
        int find(int p){
            assert( p >= 0 && p < count );
            // 不断去查询自己的父亲节点, 直到到达根节点
            // 根节点的特点: parent[p] == p
            while( p != parent[p] )
                p = parent[p];
            return p;
        }

        // 查看元素p和元素q是否所属一个集合
        // O(h)复杂度, h为树的高度
        bool isConnected( int p , int q ){
            return find(p) == find(q);
        }

        // 合并元素p和元素q所属的集合
        // O(h)复杂度, h为树的高度
        void unionElements(int p, int q){

            int pRoot = find(p);
            int qRoot = find(q);

            if( pRoot == qRoot )
                return;

            // 根据两个元素所在树的元素个数不同判断合并方向
            // 将元素个数少的集合合并到元素个数多的集合上
            if( rank[pRoot] < rank[qRoot] ){
                parent[pRoot] = qRoot;
            }
            else if( rank[qRoot] < rank[pRoot]){
                parent[qRoot] = pRoot;
            }
            else{ // rank[pRoot] == rank[qRoot]
                parent[pRoot] = qRoot;
                rank[qRoot] += 1;   // 此时, 我维护rank的值
            }
        }
    };
}

3 路径压缩并查集

路径压缩

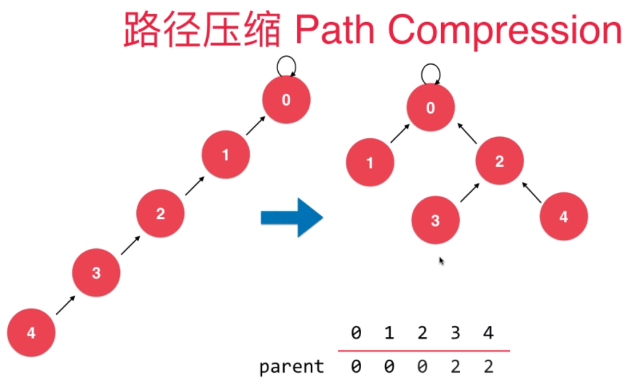
路径压缩

查找根节点时将父节点指向父节点的父节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include <cassert>

using namespace std;

namespace UF5{

    class UnionFind{

    private:
        
        int* rank;   // rank[i]表示以i为根的集合所表示的树的层数
        int* parent; // parent[i]表示第i个元素所指向的父节点
        int count;   // 数据个数

    public:
        // 构造函数
        UnionFind(int count){
            parent = new int[count];
            rank = new int[count];
            this->count = count;
            for( int i = 0 ; i < count ; i ++ ){
                parent[i] = i;
                rank[i] = 1;
            }
        }

        // 析构函数
        ~UnionFind(){
            delete[] parent;
            delete[] rank;
        }

        // 查找过程, 查找元素p所对应的集合编号
        // O(h)复杂度, h为树的高度
        int find(int p){
            assert( p >= 0 && p < count );

            // path compression 1
            while( p != parent[p] ){
                parent[p] = parent[parent[p]];
                p = parent[p];
            }
            return p;

        }

        // 查看元素p和元素q是否所属一个集合
        // O(h)复杂度, h为树的高度
        bool isConnected( int p , int q ){
            return find(p) == find(q);
        }

        // 合并元素p和元素q所属的集合
        // O(h)复杂度, h为树的高度
        void unionElements(int p, int q){

            int pRoot = find(p);
            int qRoot = find(q);

            if( pRoot == qRoot )
                return;

            // 根据两个元素所在树的元素个数不同判断合并方向
            // 将元素个数少的集合合并到元素个数多的集合上
            if( rank[pRoot] < rank[qRoot] ){
                parent[pRoot] = qRoot;
            }
            else if( rank[qRoot] < rank[pRoot]){
                parent[qRoot] = pRoot;
            }
            else{ // rank[pRoot] == rank[qRoot]
                parent[pRoot] = qRoot;
                rank[qRoot] += 1;   // 此时维护rank的值
            }
        }
    };
}