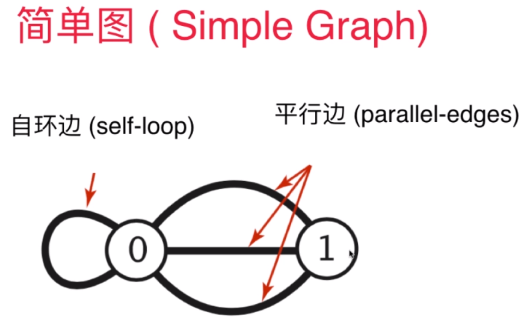
图论

分为无向图和有向图
分为有权图和无权图（边的值）
图的连通性

1 图的表示

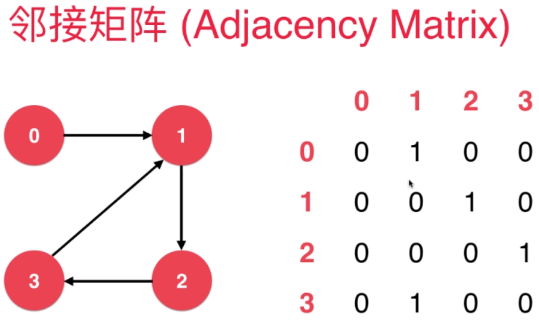
邻接矩阵

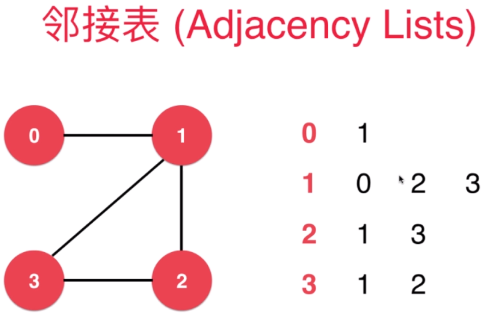
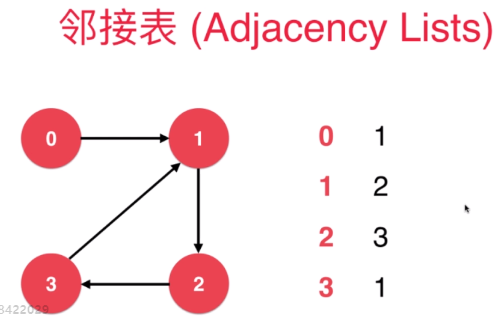
邻接表2

邻接矩阵适合表示稠密图，邻接表适合表示稀疏图。稠密与稀疏取决于边（edge）的数量。

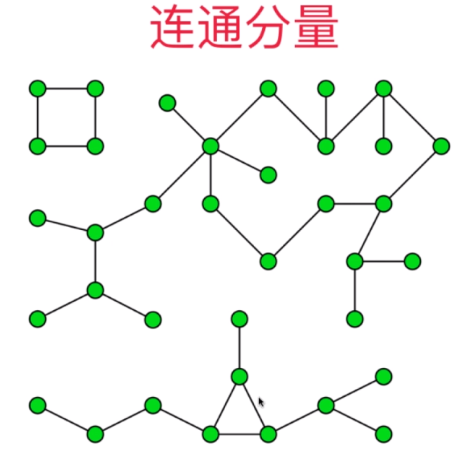
2 深度优先遍历（dfs）与连通分量（Components）

深度优先遍历与树的前序遍历类似，但需要记录该节点是否遍历过

3 寻路

与dfs相似

4 广度优先遍历（bfs）与最短路径

广度优先遍历与树的层序遍历类似，利用队列，一个节点出队，将所有相连节点加入队列，需要记录该节点是否遍历过。
广度优先遍历的特点在于先遍历的元素距离起点近（无权图）。

5 有权图（weighted graph）

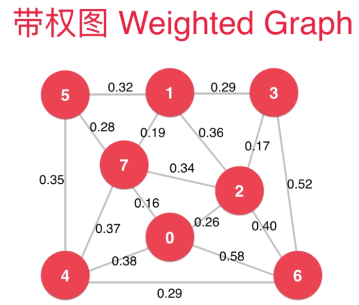
有权图

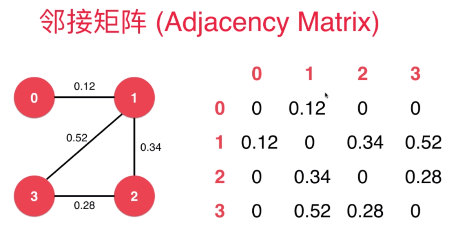
有权图邻接矩阵

有权图邻接表

6 最小生成树和切分定理（cut property）

n-1条边连接了n个节点，称为生成树。若总权值最小，称为最小生成树。
将图进行切分，边的两个节点分属两半称为横切边。
切分定理：对于任意切分，横切边中权值最小的边属于最小生成树。

7 prim算法

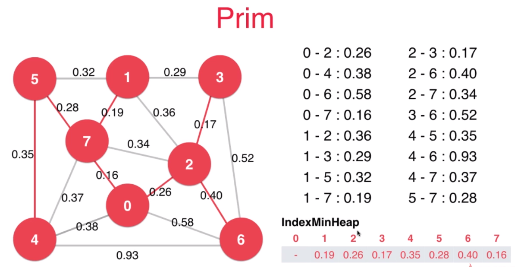
有权图邻接表

8 kruskal算法

9 最短路径问题与松弛操作（relaxation）

松弛操作是最短路径问题的核心。

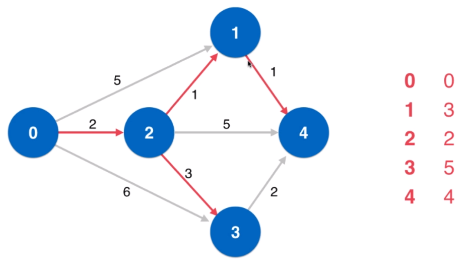
10 dijkstra算法

前提：没有负权边。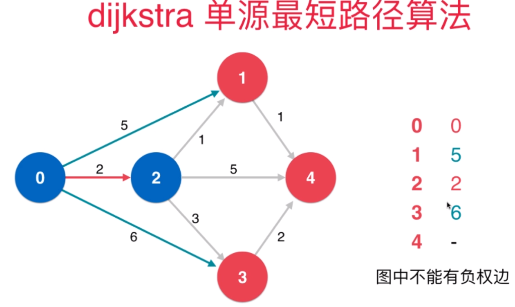

如图所示，0到2的路径最短，因此0到2的最短路径可以确定为2。

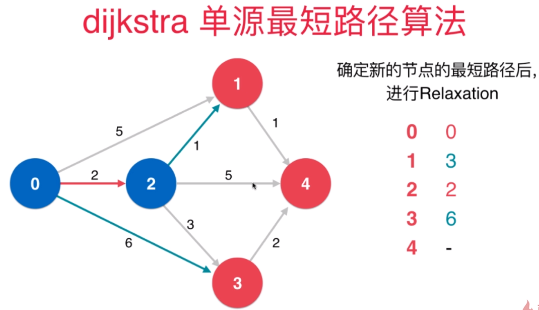
如图所示，2到1的距离是1，则0到1的最短距离更新为3，距离为5的边被废弃，这一操作为松弛操作。

通过上述两种操作，可得到如下结果。

11 负权边与bellman-ford算法

如果有负权环，则没有最短路径。
bellman-ford算法可解决负权边最短路径问题。
最短路径最多经过n个节点，否则就有负权环。
一个点的一次松弛操作就是找到经过这个点的另外一条路径，多一条边，权值更小。从一点到另外一点最多有n-1条边。对所有的点进行n-1次松弛操作，找到最短路径。如果n-1次松弛操作后还可以继续松弛，则有负权环。

12 拓扑排序

用于有向无环图

13 课程用到的算法思想

总结