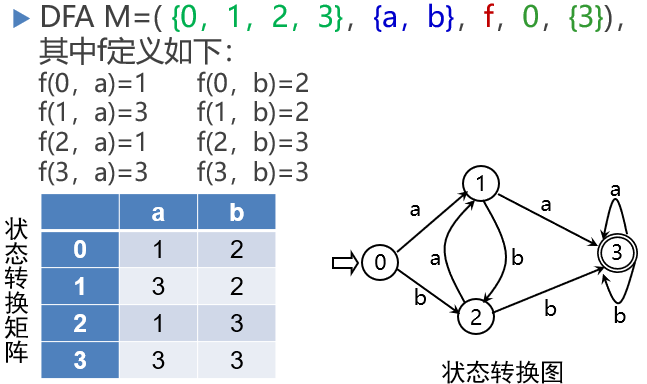
第四章 词法分析

第一部分：词法分析器的设计

1 词法分析的任务

词法分析的任务：从左至右逐个字符地对源程序进行扫描，产生一个个单词符号

词法分析器(Lexical Analyzer)：扫描器(Scanner)、执行词法分析的程序

2 词法分析器的功能

功能：输入源程序、输出单词符号

单词符号的种类：
基本字：如 begin，repeat，for，…
标识符：用来表示各种名字，如变量名、数组名和过程名
常数：各种类型的常数
运算符：+，-，*，/，…
界符：逗号、分号、括号和空白

3 词法分析器的输出

输出：输出的单词符号的表示形式(单词种别，单词自身的值)

单词种别通常用整数编码表示：
若一个种别只有一个单词符号，则种别编码就代表该单词符号。假定基本字、运算符和界符都是一符一种。
若一个种别有多个单词符号，则对于每个单词符号，给出种别编码和自身的值。

4 词法分析器在编译器中的地位

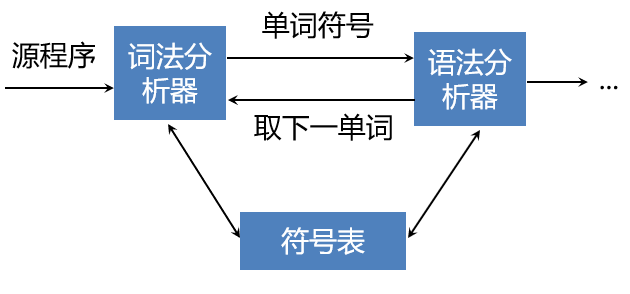
词法分析器在编译器中的地位

5 词法分析器的结构

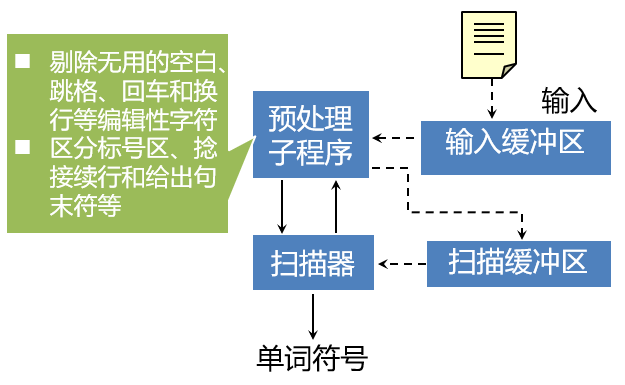
词法分析器的结构

6 避免超前搜索

所有基本字都是保留字;用户不能用它们作自己的标识符；
基本字作为特殊的标识符来处理，使用保留字表；
如果基本字、标识符和常数(或标号)之间没有确定的运算符或界符作间隔，则必须使用一个空白符作间隔。

7 状态转换图

状态转换图是一张有限方向图。
结点代表状态，用圆圈表示；
状态之间用箭弧连结，箭弧上的标记(字符)代表射出结状态下可能出现的输入字符或字符类；
一张转换图只包含有限个状态，其中有一个为初态，至少要有一个终态。

状态转换图可用于识别(或接受)一定的字符串。
若存在一条从初态到某一终态的道路，且这条路上所有弧上的标记符连接成的字等于α，则称α被该状态转换图所识别(接受)

8 词法分析器的设计示例

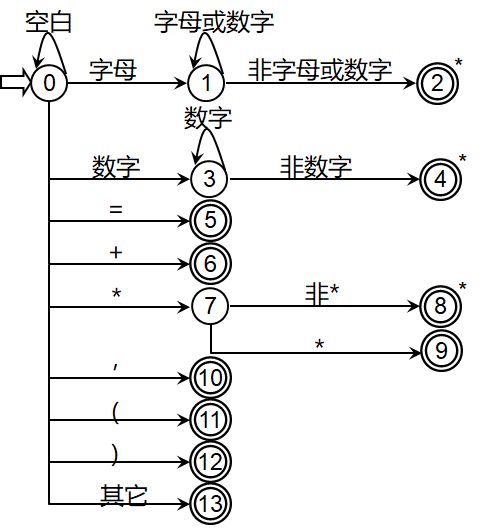
词法分析器的设计示例

9 状态转换图的程序实现

不含回路的分叉结点：可用一个CASE语句或一组IF-THEN-ELSE语句实现；
含回路的状态结点：对应一段由WHILE结构和IF语句构成的程序；
终态结点：表示识别出某种单词符号，对应返回语句。

第二部分：词法规则的形式化

10 正规式和正规集

正规集可以用正规式表示，正规式是表示正规集一种方法。
一个字集合是正规集当且仅当它能用正规式表示。
递归定义：
    ε和Ø都是Σ上的正规式，它们所表示的正规集为{ε}和Ø;
    任何a∈Σ，a是Σ上的正规式，它所表示的正规集为{a};
    假定e1和e2都是上的正规式，它们所表示的正规集为L(e1)和L(e2)，则：(e1|e2)为正规式，它所表示的正规集为L(e1)∪L(e2)，(e1.e2)为正规式，它所表示的正规集为L(e1)L(e2)，(e1)*为正规式，它所表示的正规集为(L(e1))*。

若两个正规式所表示的正规集相同，则称这两个正规式等价。

正规式满足交换律、结合律、分配律。但e1e2 <> e2e1。

11 确定有限自动机(DFA)

确定有限自动机(Deterministic Finite Automata，DFA) M是一个五元式，M=(S, Σ, f, S0, F)，其中：
S：有穷状态集；
Σ：输入字母表(有穷)；
f：状态转换函数，为S×Σ→S的单值部分映射，f(s，a)=s’表示：当现行状态为s，输入字符为a时，将状态转换到下一状态s’，s’称为s的一个后继状态；
S0∈S是唯一的一个初态；
F⊆S：终态集(可空)。

例如：

对于Σ*中的任何字α，若存在一条从初态到某一终态的道路，且这条路上所有弧上的标记符连接成的字等于α，则称α为DFA M所识别(接收)。
DFA M所识别的字的全体记为L(M)。

12 非确定有限自动机(NFA)

非确定有限自动机(Nondeterministic Finite Automata，NFA) M是一个五元式M=(S, Σ, f, S0, F)，其中：
S：有穷状态集
Σ：输入字母表(有穷)
f：状态转换函数，为S×Σ*→2S的部分映射
S0⊆S是非空的初态集
F⊆S：终态集(可空)

NFA 和DFA的区别：
NFA可以有多个初态；
弧上的标记可以是Σ*中的一个字(甚至可以是一个正规式)，而不一定是单个字符；
同一个字可能出现在同状态射出的多条弧上。

13 DFA和NFA

对于任何两个有限自动机M和M’，如果L(M)=L(M’)，则称M与M’等价。
自动机理论中一个重要的结论：判定两个自动机等价性的算法是存在的。
对于每个NFA M存在一个DFA M’，使得 L(M)=L(M’)。
DFA与NFA识别能力相同。

第三部分：有限自动机的等价性

14 DFA的化简

对于给定的DFA M，寻找一个状态数比M少的DFA M’，使得L(M)=L(M’)。

状态的等价性：
假设s和t为M的两个状态，如果从状态s出发能读出某个字α而停止于终态，那么同样，从t出发也能读出α而停止于终态；反之亦然，称s和t等价；
两个状态不等价，则称它们是可区别的。

基本思想：
把M的状态集划分为一些不相交的子集，使得任何两个不同子集的状态是可区别的，而同一子集的任何两个状态是等价的。
最后，让每个子集选出一个代表，同时消去其他状态。

子集划分：
首先，把S划分为终态和非终态两个子集，形成基本划分Π；
假定到某个时候，Π已含m个子集，记为Π={I(1)，I(2)，…，I(m)}，检查Π中的每个子集看是否能进一步划分；
一般地，对某个a和I(i)，若Ia(i) 落入现行Π中N个不同子集，则应把I(i)划分成N个不相交的组，使得每个组J的Ja都落入的Π同一子集；
重复上述过程，直到Π所含子集数不再增长；
对于上述最后划分Π中的每个子集，我们选取每个子集I中的一个状态代表其他状态，则可得到化简后的DFA M’；
若I含有原来的初态，则其代表为新的初态，若I含有原来的终态，则其代表为新的终态。

15 NFA与正规式的转换

对转换图概念拓广，令每条弧可用一个正规式作标记。

1. 对任何FA M，都存在一个正规式r，使得L(r)=L(M)。
2. 对任何正规式r，都存在一个FA M，使得L(M)=L(r)。

状态转换图消去结点的方法：

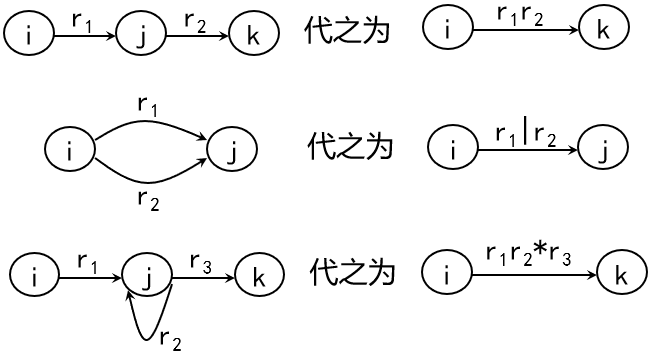
状态转换图消去结点的方法

16 词法分析程序自动生成–LEX

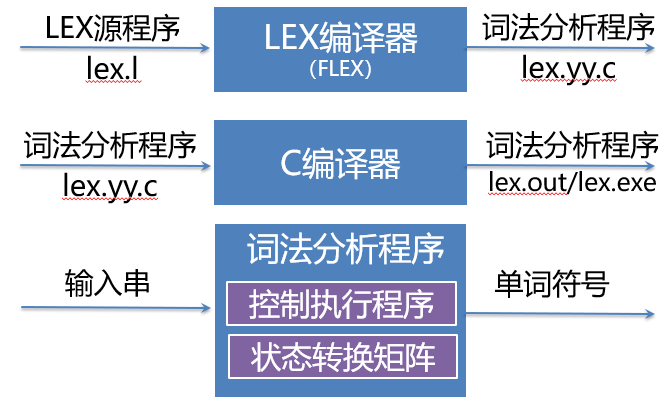
词法分析程序自动生成--LEX

工作过程：
对每条识别规则Pi构造一个相应的非确定有限自动机Mi；
引进一个新初态X，通过弧，将这些自动机连接成一个新的NFA；
把M确定化、最小化，生成该DFA的状态转换表和控制执行程序。