数据结构课程笔记

第一章绪论

1 最大子列和问题

给定K个整数组成的序列{ N1, N2, …, NK }，“连续子列”被定义为{ Ni, Ni+1, …, Nj }，其中 1≤i≤j≤K。“最大子列和”则被定义为所有连续子列元素的和中最大者。例如给定序列{ -2, 11, -4, 13, -5, -2 }，其连续子列{ 11, -4, 13 }有最大的和20。现要求你编写程序，计算给定整数序列的最大子列和。

输入格式:
输入第1行给出正整数K (≤100000)；第2行给出K个整数，其间以空格分隔。
输入样例：

1 2	6 -2 11 -4 13 -5 -2

输出格式:
在一行中输出最大子列和。如果序列中所有整数皆为负数，则输出0。
输出样例：

#include<stdio.h>
int main(){
    int result=0,thissum=0,N,digit;
    scanf("%d",&N);
    for(int i=0;i<N;i++){
        scanf("%d",&digit);
        thissum+=digit;
        if(thissum>result)
            result=thissum;
        if(thissum<0)   thissum=0;
    }
    printf("%d",result);
    return 0;
}

2 最大子列和问题

输入格式:
输入第1行给出正整数K (≤100000)；第2行给出K个整数，其间以空格分隔。
输入样例：

1 2	10 -10 1 2 3 4 -5 -23 3 7 -21

输出格式:
对于每个测试用例，在一行中输出最大和，以及最大子序列的第一个和最后一个数字。数字必须用一个空格隔开，但行尾不能有多余的空格。如果最大子序列不唯一，则输出索引i和j最小的子序列（如示例所示）。如果所有K个数都是负数，那么它的最大和被定义为0，你应该输出整个序列的第一个和最后一个数。
输出样例：

10 1 4

#include<stdio.h>
int main() {
    int result = 0, thissum = 0, N, digit, startnew = 0, start = 0, end, trigger = 0;
    if (scanf("%d", &N)) {};
    end = N -1;
    for (int i = 0; i < N; i++) {
        if (scanf("%d", &digit)) {};
        thissum += digit;
        if (thissum > result) {
            if (trigger == 1) {
                trigger = 0;
                start = digit;
            }
            end = digit;
            result = thissum;
        }
        if (thissum < 0) {
            trigger = 1;
            thissum = 0;
        }
    }
    printf("%d %d %d\n", result, start, end);
    return 0;
}

第二章线性结构

1 一元多项式的乘法与加法运算

设计函数分别求两个一元多项式的乘积与和。

输入格式:
输入分2行，每行分别先给出多项式非零项的个数，再以指数递降方式输入一个多项式非零项系数和指数（绝对值均为不超过1000的整数）。数字间以空格分隔。
输入样例：

1 2	4 3 4 -5 2 6 1 -2 0 3 5 20 -7 4 3 1

输出格式:
输出分2行，分别以指数递降方式输出乘积多项式以及和多项式非零项的系数和指数。数字间以空格分隔，但结尾不能有多余空格。零多项式应输出0 0。
输出样例：

1 2	15 24 -25 22 30 21 -10 20 -21 8 35 6 -33 5 14 4 -15 3 18 2 -6 1 5 20 -4 4 -5 2 9 1 -2 0

#include<stdio.h>
#include<stdlib.h>
#include<string.h>

typedef struct PolyNode *Polynomial;
struct PolyNode {
    int coef;
    int expon;
    Polynomial link;
};

void Attach(int c, int e, Polynomial* pRear)
{
    Polynomial P;

    P = (Polynomial)malloc(sizeof(struct PolyNode));
    P->coef = c;
    P->expon = e;
    P->link = NULL;
    (*pRear)->link = P;
    *pRear = P;
}

Polynomial ReadPoly()
{
    Polynomial P, Rear, t;
    int c, e, N;

    scanf("%d", &N);
    P = (Polynomial)malloc(sizeof(struct PolyNode)); //表头空结点
    P->link = NULL;
    Rear = P;
    while (N--) {
        scanf("%d %d", &c, &e);
        if (c != 0)       
            Attach(c, e, &Rear);    //当前项插入尾部
    }
    t = P; P = P->link; free(t);  //删除临时头结点
    return P;
}

int Compare(int e1, int e2)
{ /*比较两项指数e1和e2，根据大、小、等三种情况分别返回1，-1，0 */
    if (e1 > e2) return 1;       /* e1大，返回1       */
    else if (e1 < e2) return -1; /* e2大，返回-1      */
    else  return 0;                /* e1和e2相等，返回0 */
}

Polynomial Add(Polynomial P1, Polynomial P2)
{
    Polynomial front, rear, temp;
    int sum;
    rear = (Polynomial)malloc(sizeof(struct PolyNode));
    front = rear;
    while (P1 && P2)
    {
        switch (Compare(P1->expon, P2->expon))
        {
        case 1:
            Attach(P1->coef, P1->expon, &rear);
            P1 = P1->link;
            break;
        case -1:
            Attach(P2->coef, P2->expon, &rear);
            P2 = P2->link;
            break;
        case 0:
            sum = P1->coef + P2->coef;
            if (sum) Attach(sum, P1->expon, &rear);
            P1 = P1->link;
            P2 = P2->link;
            break;
        }
    }
    for (; P1; P1 = P1->link) Attach(P1->coef, P1->expon, &rear);
    for (; P2; P2 = P2->link) Attach(P2->coef, P2->expon, &rear);
    rear->link = NULL;
    temp = front;
    front = front->link;
    free(temp);
    return front;
}

Polynomial Mult(Polynomial P1, Polynomial P2)
{
    Polynomial P, Rear, t1, t2, t;
    int c, e;

    if (!P1 || !P2) return NULL;

    t1 = P1; t2 = P2;
    P = (Polynomial)malloc(sizeof(struct PolyNode)); P->link = NULL;
    Rear = P;
    while (t2)   //先使用P1第一项乘P2得到初始链表
    {
        Attach(t1->coef * t2->coef, t1->expon + t2->expon, &Rear);
        t2 = t2->link;
    }
    t1 = t1->link;
    while (t1)
    {
        t2 = P2; Rear = P;
        while (t2)
        {
            e = t1->expon + t2->expon;
            c = t1->coef * t2->coef;
            while (Rear->link && Rear->link->expon > e)
                Rear = Rear->link;
            if (Rear->link && Rear->link->expon == e)  //与下一个相等
            {
                if (Rear->link->coef + c)
                    Rear->link->coef += c;
                else {
                    t = Rear->link;
                    Rear->link = t->link;
                    free(t);
                }
            }
            else                                //比下一个大
            {
                t = (Polynomial)malloc(sizeof(struct PolyNode));
                t->coef = c; t->expon = e; t->link = Rear->link;
                Rear->link = t; Rear = Rear->link;
            }
            t2 = t2->link;
        }
        t1 = t1->link;
    }
    t2 = P; P = P->link; free(t2);

    return P;
}

void PrintPoly(Polynomial P)
{
    int c, e, flag = 0;

    if (!P) { printf("0 0"); return; }

    while (P)
    {
        c = P->coef; e = P->expon;
        if (!flag)
            flag = 1;
        else
            printf(" ");
        printf("%d %d", c, e);
        P = P->link;
    }
}

int main() {
    Polynomial P1, P2, PP, PS;

    P1 = ReadPoly();
    P2 = ReadPoly();
    PP = Mult(P1, P2);
    PrintPoly(PP);
    printf("\n");
    PS = Add(P1, P2);
    PrintPoly(PS);

    return 0;
}

2 两个有序链表序列的合并

本题要求实现一个函数，将两个链表表示的递增整数序列合并为一个非递减的整数序列。
L1和L2是给定的带头结点的单链表，其结点存储的数据是递增有序的；函数Merge要将L1和L2合并为一个非递减的整数序列。应直接使用原序列中的结点，返回归并后的带头结点的链表头指针。

输入样例：

输出样例：

1
2
3

1 2 3 4 5 6 8 10 
NULL
NULL

#include <stdio.h>
#include <stdlib.h>

typedef int ElementType;
typedef struct Node* PtrToNode;
struct Node {
    ElementType Data;
    PtrToNode   Next;
};
typedef PtrToNode List;

List Read(); /* 细节在此不表 */
void Print(List L); /* 细节在此不表；空链表将输出NULL */

List Merge(List L1, List L2);

int main()
{
    List L1, L2, L;
    L1 = Read();
    L2 = Read();
    L = Merge(L1, L2);
    Print(L);
    Print(L1);
    Print(L2);
    return 0;
}

void Attach(int d, List* pRear)
{
    List P;

    P = (List)malloc(sizeof(struct Node));
    P->Data = d;
    P->Next = NULL;
    (*pRear)->Next = P;
    *pRear = P;
}

List Merge(List L1, List L2)
{
    List temp1 = L1->Next;
    List temp2 = L2->Next;
    List p;
    p = (List)malloc(sizeof(struct Node));
    p->Next = NULL;
    List temp = p;
    while (temp1 && temp2) {
        if (temp1->Data < temp2->Data) {
            temp->Next = temp1;
            temp1 = temp1->Next;
            temp = temp->Next;
        }
        else {

            temp->Next = temp2;
            temp2 = temp2->Next;
            temp = temp->Next;
        }

    }
    while (temp1 != NULL) {
        temp->Next = temp1;
        temp1 = temp1->Next;
        temp = temp->Next;
    }
    while (temp2 != NULL) {
        temp->Next = temp2;
        temp2 = temp2->Next;
        temp = temp->Next;
    }
    L1->Next = NULL;
    L2->Next = NULL;
    temp->Next = NULL;
    return p;
}


List Read()
{
    List P, Rear, t;
    int d, N;

    scanf("%d", &N);
    P = (List)malloc(sizeof(struct Node)); //表头空结点
    P->Next = NULL;
    Rear = P;
    while (N--) {
        scanf("%d", &d);
        Attach(d, &Rear);    //当前项插入尾部
    }
    return P;
}

void Print(List L) {
    if (L->Next == NULL) {
        printf("NULL\n");
        return;
    }
    List temp = L->Next;
    while (temp) {
        printf("%d ", temp->Data);
        temp = temp->Next;
    }
    printf("\n");
}

3 Pop Sequence

给定一个最多能保存M个数的堆栈。按1，2，3，…，N的顺序推N个数字，然后随机弹出。您应该知道给定的数字序列是否可能是堆栈的弹出序列。例如，如果M是5，N是7，我们可以从堆栈中获得1，2，3，4，5，6，7，但不能从3，2，1，7，5，6，4。

输入格式:
每个输入文件包含一个测试用例。对于每种情况，第一行包含3个数字（都不超过1000）：M（堆栈的最大容量）、N（推送序列的长度）和K（要检查的pop序列的数量）。接下来是K行，每行包含N个数字的pop序列。一行中的所有数字都用空格隔开。
输入样例：

5 7 5
1 2 3 4 5 6 7
3 2 1 7 5 6 4
7 6 5 4 3 2 1
5 6 4 3 7 2 1
1 7 6 5 4 3 2

输出格式:
对于每个弹出序列，如果确实是堆栈的可能弹出序列，则在一行中打印“YES”，如果不是，则打印“NO”。
输出样例：

YES
NO
NO
YES
NO

#include <stdio.h>
#include <stdlib.h>

int main()
{
    int i, j, m, n, k, a[1000][1000], b[1000], stack[1000], stack_index, top;
    scanf("%d %d %d", &m, &n, &k);
    for (i = 0; i < k; i++)
    {
        
        for (j = 0; j < n; j++)    //读取每一行
        {
            scanf("%d", &a[i][j]);                   
        }
        stack_index = 1;      //模拟栈
        top = 1;
        stack[1] = 1;
        for (j = 0; j < n; j++)
        {
            while (a[i][j] > top)
            {
                stack_index++;
                top++;
                stack[stack_index] = top;
            }
            if (stack_index > m || a[i][j] < stack[stack_index])
            {
                b[i] = 0;       //无法实现栈则结果为0，退出
                break;
            }
            if (a[i][j] == stack[stack_index])
            {
                stack_index--;
                //top = stack[stack_index];
            }
        }
        if (stack_index == 0)   //成功实现栈则结果为1
            b[i] = 1;
    }
    for (i = 0; i < k; i++)
    {
        if (b[i] == 0)
            printf("NO");
        else if (b[i] == 1)
            printf("YES");
        printf("\n");
    }   
    return 0;
}

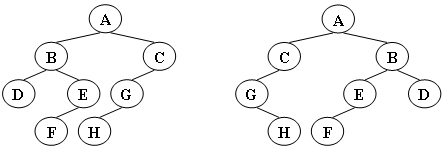
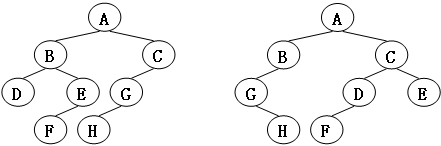
第三章树结构（上）

1 树的同构

给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的，因为我们把其中一棵树的结点A、B、G的左右孩子互换后，就得到另外一棵树。而图2就不是同构的。

图1

图2
输入格式:
输入给出2棵二叉树树的信息。对于每棵树，首先在一行中给出一个非负整数N (≤10)，即该树的结点数（此时假设结点从0到N−1编号）；随后N行，第i行对应编号第i个结点，给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空，则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意：题目保证每个结点中存储的字母是不同的。

输出格式:
如果两棵树是同构的，输出“Yes”，否则输出“No”。

输入样例1（对应图1）：

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

输出样例1（对应图1）：

Yes

输入样例2（对应图2）：

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

输出样例2（对应图2）：

No

import java.util.Arrays;
import java.util.Scanner;

class TreeNode {
    String val;
    int left;
    int right;
}

public class Main {
    private static TreeNode[] T1 = new TreeNode[10];
    private static TreeNode[] T2 = new TreeNode[10];
    private static int[] check = new int[10];

    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int T = scan.nextInt();
        Arrays.fill(check, 0);
        for (int i = 0; i < T; i++) {
            T1[i] = new TreeNode();
            T1[i].val = scan.next();
            String left = scan.next();
            String right = scan.next();
            if (left.equals("-")) {
                T1[i].left = -1;
            } else {
                T1[i].left = Integer.parseInt(left);
                check[Integer.parseInt(left)] = 1;
            }

            if (right.equals("-")) {
                T1[i].right = -1;
            } else {
                T1[i].right = Integer.parseInt(right);
                check[Integer.parseInt(right)] = 1;
            }
        }

        int root = -1;
        for (int i = 0; i < T; i++) {
            if (check[i] == 0) {
                root = i;
            }
        }

        T = scan.nextInt();
        Arrays.fill(check, 0);
        for (int i = 0; i < T; i++) {
            T2[i] = new TreeNode();
            T2[i].val = scan.next();
            String left = scan.next();
            String right = scan.next();
            if (left.equals("-")) {
                T2[i].left = -1;
            } else {
                T2[i].left = Integer.parseInt(left);
                check[Integer.parseInt(left)] = 1;
            }

            if (right.equals("-")) {
                T2[i].right = -1;
            } else {
                T2[i].right = Integer.parseInt(right);
                check[Integer.parseInt(right)] = 1;
            }
        }

        int root1 = -1;
        for (int i = 0; i < T; i++) {
            if (check[i] == 0) {
                root1 = i;
            }
        }
        System.out.println(Isomorphic(root, root1) ? "Yes" : "No");
    }
    //传递进来root的索引值可以避免数组越界
    public static boolean Isomorphic(int node1, int node2) {
        if (node1 == -1 && node2 == -1) {
            return true;
        }
        if ((node1 == -1 && node2 != -1) || (node1 != -1 && node2 == -1) || (!T1[node1].val.equals(T2[node2].val))) {
            return false;
        }
        if (T1[node1].left == -1 && T2[node2].left == -1) {
            return Isomorphic(T1[node1].right, T2[node2].right);
        }
        if ((T1[node1].left != -1 && T2[node2].left != -1) && T1[T1[node1].left].val.equals(T2[T2[node2].left].val)) {
            return (Isomorphic(T1[node1].left, T2[node2].left) && Isomorphic(T1[node1].right, T2[node2].right));
        } else {
            return (Isomorphic(T1[node1].left, T2[node2].right) && Isomorphic(T1[node1].right, T2[node2].left));
        }
    }
}

2 List Leaves

给定一棵树，您应该按照从上到下，从左到右的顺序列出所有叶子。

输入格式:
每个输入文件包含一个测试用例。对于每种情况，第一行给出一个正整数N（≤ 1 0），这是树中的节点的总数-并且因此节点编号从0到N − 1。然后N行跟随，每行对应一个节点，并给出该节点的左，右子级的索引。如果孩子不存在，将在该位置放置一个“-”。任何一对孩子都用空格隔开。

输出格式:
对于每个测试用例，按从上到下，从左到右的顺序在一行中打印所有叶子的索引。相邻数字之间必须恰好有一个空格，并且在行尾不能有多余的空格。

输入样例：

8
1 -
- -
0 -
2 7
- -
- -
5 -
4 6

输出样例：

4 1 5

import java.util.Arrays;
import java.util.Scanner;
import java.util.LinkedList;
import java.util.Queue;

class TreeNode {
    int left;
    int right;
}

public class Main {
    private static TreeNode[] tree = new TreeNode[10];
    private static int[] check = new int[10];
    private static Queue<Integer> queue = new LinkedList<Integer>();
    private static boolean flag = false;

    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int T = scan.nextInt();
        Arrays.fill(check, 0);
        for (int i = 0; i < T; i++) {
            tree[i] = new TreeNode();
            String left = scan.next();
            String right = scan.next();
            if (left.equals("-")) {
                tree[i].left = -1;
            } else {
                tree[i].left = Integer.parseInt(left);
                check[Integer.parseInt(left)] = 1;
            }

            if (right.equals("-")) {
                tree[i].right = -1;
            } else {
                tree[i].right = Integer.parseInt(right);
                check[Integer.parseInt(right)] = 1;
            }
        }

        int root = -1;
        for (int i = 0; i < T; i++) {
            if (check[i] == 0) {
                root = i;
            }
        }
        printLeaves(root);
    }
    public static void printLeaves(int node) {
        if (tree[node].left != -1) {
            queue.offer(tree[node].left);
        }
        if (tree[node].right != -1) {
            queue.offer(tree[node].right);
        }
        if (tree[node].left == -1 && tree[node].right == -1) {
            if (flag) {
                System.out.print(" " + node);
            } else {
                flag = true;
                System.out.print(node);
            }
        }
        Object n = queue.poll();
        if (n == null) {
            return;
        } else {
            printLeaves((int)n);
        }
    }
}

第四章树（中）

1 是否同一棵二叉搜索树

给定一个插入序列就可以唯一确定一棵二叉搜索树。然而，一棵给定的二叉搜索树却可以由多种不同的插入序列得到。例如分别按照序列{2, 1, 3}和{2, 3, 1}插入初始为空的二叉搜索树，都得到一样的结果。于是对于输入的各种插入序列，你需要判断它们是否能生成一样的二叉搜索树。

输入格式:

输入包含若干组测试数据。每组数据的第1行给出两个正整数N (≤10)和L，分别是每个序列插入元素的个数和需要检查的序列个数。第2行给出N个以空格分隔的正整数，作为初始插入序列。最后L行，每行给出N个插入的元素，属于L个需要检查的序列。
简单起见，我们保证每个插入序列都是1到N的一个排列。当读到N为0时，标志输入结束，这组数据不要处理。

输入样例：

输出格式:

对每一组需要检查的序列，如果其生成的二叉搜索树跟对应的初始序列生成的一样，输出“Yes”，否则输出“No”。

输出样例：

1
2
3

Yes
No
No

import java.util.Scanner;

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    boolean flag;
}

public class Main {

    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int N = scan.nextInt();
        while (N != 0) {
            int L = scan.nextInt();

            //以第一行数据创建树
            TreeNode root = new TreeNode();
            root.val = scan.nextInt();
            for (int i = 1; i < N; i++) {
                int val = scan.nextInt();
                root = Insert(root, val);
            }

            //将后L行数据与第一行对比
            for (int i = 0; i < L; i++) {
                boolean flag = true;
                int val = scan.nextInt();
                if (val != root.val) {
                    flag = false;
                } else {
                    root.flag = true;
                }
                for (int j = 1; j < N; j++) {
                    int nextVal = scan.nextInt();
                    if (flag) {
                        flag = Check(root, nextVal);
                    }
                }
                if (flag) {
                    System.out.println("Yes");
                } else {
                    System.out.println("No");
                }
                Reset(root);
            }

            N = scan.nextInt();
        }
    }

    //增加节点
    private static TreeNode Insert(TreeNode node, int val) {
        if (node == null) {
            node = new TreeNode();
            node.val = val;
        } else {
            if (val < node.val) {
                node.left = Insert(node.left, val);
            } else if (val > node.val) {
                node.right = Insert(node.right, val);
            }
        }
        return node;
    }

    //检查节点是否位置对应相等
    private static boolean Check(TreeNode node, int val) {
        if (node.flag) {
            if (val < node.val) {
                return Check(node.left, val);
            } else if (val > node.val) {
                return Check(node.right, val);
            } else {
                return false;
            }
        } else {
            if (val == node.val) {
                node.flag = true;
                return true;
            } else {
                return false;
            }
        }
    }

    //复位树的flag
    private static void Reset(TreeNode node) {
        if (node.left != null) {
            Reset(node.left);
        }
        if (node.right != null) {
            Reset(node.right);
        }
        node.flag = false;
    }
}

第五章树（下）

1 堆中的路径

将一系列给定数字插入一个初始为空的最小堆H[]。随后对任意给定的下标i，打印从H[i]到根结点的路径。

输入格式:

每组测试第1行包含2个正整数N和M(≤1000)，分别是插入元素的个数、以及需要打印的路径条数。下一行给出区间[-10000, 10000]内的N个要被插入一个初始为空的小顶堆的整数。最后一行给出M个下标。

输入样例：

1
2
3

5 3
46 23 26 24 10
5 4 3

输出格式:

对输入中给出的每个下标i，在一行中输出从H[i]到根结点的路径上的数据。数字间以1个空格分隔，行末不得有多余空格。

输出样例：

1
2
3

24 23 10
46 23 10
26 10

import java.util.Scanner;

class Heap {
    int[] heap;        /* 存储元素的数组 */
    int size;          /* 堆中当前元素个数 */
    int capacity;      /* 堆的最大容量 */
}

public class Main {

    public static void main (String[] args) {
        Scanner scan = new Scanner(System.in);
        int N = scan.nextInt();
        int M = scan.nextInt();
        Heap minHeap = new Heap();
        minHeap.heap = new int[N + 1];
        minHeap.size = 0;
        minHeap.capacity = N;
        minHeap.heap[0] = -20000; //哨兵
        for (int i = 0; i < N; i++) {
            minHeap = Insert(minHeap, scan.nextInt());
        }
        for (int i = 0; i < M; i++) {
            for (int index = scan.nextInt(); index > 0; index /= 2) {
                if (index == 1) {
                    System.out.print(minHeap.heap[index]);
                } else {
                    System.out.print(minHeap.heap[index] + " ");
                }
            }
            if (i != M - 1)
                System.out.print("\n");
        }
    }

    //增加最小堆节点
    private static Heap Insert(Heap minHeap, int val) {
        if (minHeap.size < minHeap.capacity) {
            int i = ++minHeap.size;
            for ( ; minHeap.heap[i / 2] > val; i /= 2) {
                minHeap.heap[i] = minHeap.heap[i / 2];
            }
            minHeap.heap[i] = val;
        }
        return minHeap;
    }
}

第六章图（上）

1 列出连通集

给定一个有N个顶点和E条边的无向图，请用DFS和BFS分别列出其所有的连通集。假设顶点从0到N−1编号。进行搜索时，假设我们总是从编号最小的顶点出发，按编号递增的顺序访问邻接点。

输入格式:
输入第1行给出2个整数N(0<N≤10)和E，分别是图的顶点数和边数。随后E行，每行给出一条边的两个端点。每行中的数字之间用1空格分隔。
输入样例：

输出格式:
按照”{ v1 v2 … vk }”的格式，每行输出一个连通集。先输出DFS的结果，再输出BFS的结果。
输出样例：

{ 0 1 4 2 7 }
{ 3 5 }
{ 6 }
{ 0 1 2 7 4 }
{ 3 5 }
{ 6 }

import java.util.Scanner;
import java.util.LinkedList;
import java.util.Queue;

//图
class LGraph {
    int Nv;     /* 顶点数 */
    int Ne;     /* 边数   */
    int [][]  map = new  int [10][10]; /*邻接矩阵  */
}

public class Main {
    private static Queue<Integer> queue = new LinkedList<Integer>();
    private static boolean[] Visited1 = new boolean[10];
    private static boolean[] Visited2 = new boolean[10];
    public static LGraph Graph = new LGraph();

    public static void main(String[] args) {

        Scanner scan = new Scanner(System.in);
        Graph.Nv = scan.nextInt();
        Graph.Ne = scan.nextInt();

        //图初始化
        for (int i = 0; i < Graph.Ne; i++) {
            int V1 = Integer.parseInt(scan.next());
            int V2 = Integer.parseInt(scan.next());
            if (V1 == V2)
                continue;
            Graph.map[V1][V2] = 1;
            Graph.map[V2][V1] = 1;
        }

        for (int i = 0; i < Graph.Nv; i++) {
            if (!Visited1[i]) {
                System.out.print("{ ");
                DFS(i);
                System.out.print("}\n");
            }
        }

        for (int i = 0; i < Graph.Nv; i++) {
            if (!Visited2[i]) {
                System.out.print("{ ");
                BFS(i);
                System.out.print("}\n");
            }
        }
    }

    public static void DFS (int node) {
        Visited1[node] = true;
        System.out.print(node + " ");
        for (int i =0; i < Graph.Nv; i++) {
            if (Graph.map[node][i] == 1 && !Visited1[i])
                DFS(i);
        }
    }

    public static void BFS (int node) {
        queue.offer(node);
        while (!queue.isEmpty()) {
            int n = queue.poll();
            if (!Visited2[n]) {
                Visited2[n] = true;
                System.out.print(n + " ");
            }
            for (int i =0; i < Graph.Nv; i++) {
                if (Graph.map[n][i] == 1 && !Visited2[i])
                    queue.offer(i);
            }
        }
    }
}

2 六度空间

“六度空间”理论又称作“六度分隔（Six Degrees of Separation）”理论。这个理论可以通俗地阐述为：“你和任何一个陌生人之间所间隔的人不会超过六个，也就是说，最多通过五个人你就能够认识任何一个陌生人。”

假如给你一个社交网络图，请你对每个节点计算符合“六度空间”理论的结点占结点总数的百分比。

输入格式:
输入第1行给出两个正整数，分别表示社交网络图的结点数N（1<N≤10³，表示人数）、边数M（≤33×N，表示社交关系数）。随后的M行对应M条边，每行给出一对正整数，分别是该条边直接连通的两个结点的编号（节点从1到N编号）。
输入样例：

输出格式:
对每个结点输出与该结点距离不超过6的结点数占结点总数的百分比，精确到小数点后2位。每个结节点输出一行，格式为“结点编号:（空格）百分比%”。
输出样例：

1: 70.00%
2: 80.00%
3: 90.00%
4: 100.00%
5: 100.00%
6: 100.00%
7: 100.00%
8: 90.00%
9: 80.00%
10: 70.00%

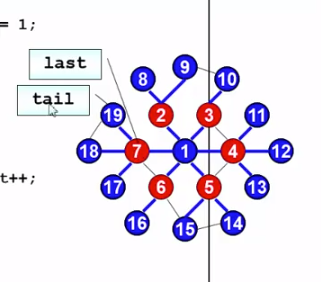
import java.util.Scanner;
import java.util.LinkedList;
import java.util.Queue;

//图
class LGraph {
    int Nv;     /* 顶点数 */
    int Ne;     /* 边数   */
    Vertex[] vertexArray = new Vertex[1000]; /*邻接表 */
}

class Vertex {
    int verName;
    Vertex nextNode;
}

public class Main {
    private static Queue<Integer> queue = new LinkedList<Integer>();
    private static boolean[] Visited = new boolean[1000];
    public static LGraph Graph = new LGraph();

    public static void main(String[] args) {

        Scanner scan = new Scanner(System.in);
        Graph.Nv = scan.nextInt();
        Graph.Ne = scan.nextInt();

        for (int i = 0; i < Graph.Ne; i++) {
            int v1 = Integer.parseInt(scan.next()) - 1;
            int v2 = Integer.parseInt(scan.next()) - 1;
            if (v1 == v2)
                continue;
            Vertex VN1 = new Vertex();
            VN1.verName = v2;
            Vertex VN2 = new Vertex();
            VN2.verName = v1;
            Vertex VN = Graph.vertexArray[v1];
            Graph.vertexArray[v1] = VN1;
            VN1.nextNode = VN;
            VN = Graph.vertexArray[v2];
            Graph.vertexArray[v2] = VN2;
            VN2.nextNode = VN;
        }

        for (int i = 0; i < Graph.Nv; i++) {
            for (int j = 0; j < Graph.Nv; j++)
                Visited[j] = false;
            int x = i + 1;
            System.out.print(x + ": ");
            BFS(i);
            if (i != Graph.Nv - 1) {
                System.out.print("\n");
            }
        }
    }

    public static void BFS (int node) {
        int count = 0, tail = 0, last = node, level = 0;
        queue.offer(node);
        while (!queue.isEmpty()) {

            int n = queue.poll();
            if (!Visited[n]) {
                count++;
                Visited[n] = true;

                Vertex no = Graph.vertexArray[n];
                while (no != null) {
                    if (!Visited[no.verName]) {
                        queue.offer(no.verName);
                        tail = no.verName;

                    }
                    no = no.nextNode;


                }
                if (n == last) {
                    last = tail;
                    level++;
                }
                if (level == 7) {
                    queue.clear();
                    break;
                }
            }
        }
        double rate = (double) count * 100 / Graph.Nv;
        System.out.print(String.format("%.2f", rate) + "%");
    }
}

小技巧：利用tail和last记录BFS当前层数

第九章排序(上)

1 排序

给定N个（长整型范围内的）整数，要求输出从小到大排序后的结果。

输入格式:
输入第一行给出正整数N（≤10⁵），随后一行给出N个（长整型范围内的）整数，其间以空格分隔。
输入样例：

1 2	11 4 981 10 -17 0 -20 29 50 8 43 -5

输出格式:
在一行中输出从小到大排序后的结果，数字间以1个空格分隔，行末不得有多余空格。
输出样例：

1	-20 -17 -5 0 4 8 10 29 43 50 981


#include<stdio.h>
#include<stdlib.h>
void Merge( int A[], int TmpA[], int L, int R, int RightEnd )
{ /* 将有序的A[L]~A[R-1]和A[R]~A[RightEnd]归并成一个有序序列 */
     int LeftEnd, NumElements, Tmp;
     int i;
      
     LeftEnd = R - 1; /* 左边终点位置 */
     Tmp = L;         /* 有序序列的起始位置 */
     NumElements = RightEnd - L + 1;
      
     while( L <= LeftEnd && R <= RightEnd ) {
         if ( A[L] <= A[R] )
             TmpA[Tmp++] = A[L++]; /* 将左边元素复制到TmpA */
         else
             TmpA[Tmp++] = A[R++]; /* 将右边元素复制到TmpA */
     }
 
     while( L <= LeftEnd )
         TmpA[Tmp++] = A[L++]; /* 直接复制左边剩下的 */
     while( R <= RightEnd )
         TmpA[Tmp++] = A[R++]; /* 直接复制右边剩下的 */
          
     for( i = 0; i < NumElements; i++, RightEnd -- )
         A[RightEnd] = TmpA[RightEnd]; /* 将有序的TmpA[]复制回A[] */
}
void Merge_pass( int A[], int TmpA[], int N, int length )
{ /* 两两归并相邻有序子列 */
     int i, j;
       
     for ( i=0; i <= N-2*length; i += 2*length )
         Merge( A, TmpA, i, i+length, i+2*length-1 );
     if ( i+length < N ) /* 归并最后2个子列*/
         Merge( A, TmpA, i, i+length, N-1);
     else /* 最后只剩1个子列*/
         for ( j = i; j < N; j++ ) TmpA[j] = A[j];
}
 
void Merge_Sort( int A[], int N )
{ 
     int length; 
     int *TmpA;
      
     length = 1; /* 初始化子序列长度*/
     TmpA =(int*)  malloc( N * sizeof( int ) );
     if ( TmpA != NULL ) {
          while( length < N ) {
              Merge_pass( A, TmpA, N, length );
              length *= 2;
              Merge_pass( TmpA, A, N, length );
              length *= 2;
          }
          free( TmpA );
     }
     else printf( "空间不足" );
}
int main()
{
	/*****************************/
	// --输入--
	int N;
	int* a;
	scanf("%d",&N);
	a = new int [N];
	for (int i=0; i<N; ++i)
		scanf("%d",&a[i]);
	/*****************************/
	Merge_Sort( a, N );	
	
	// --输出--
	printf("%d",a[0]);
	for (int i=1; i<N; ++i)
		printf(" %d",a[i]);
	delete [] a;
	return 0;
}

第十章排序(下)

1 统计工龄

给定公司N名员工的工龄，要求按工龄增序输出每个工龄段有多少员工。

输入格式:
输入首先给出正整数N（≤10⁵），即员工总人数；随后给出N个整数，即每个员工的工龄，范围在[0, 50]。
输入样例：

1 2	8 10 2 0 5 7 2 5 2

输出格式:
按工龄的递增顺序输出每个工龄的员工个数，格式为：“工龄:人数”。每项占一行。如果人数为0则不输出该项。
输出样例：

0:1
2:3
5:2
7:1
10:1

package test;
import java.lang.reflect.Array;
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        int[] A = new int[51];
        Scanner scan = new Scanner(System.in);
        int N = scan.nextInt();
        for (int i = 0; i < N; i++) {
            int n = scan.nextInt();
            A[n] += 1;
        }
        for (int i = 0; i < 51; i++) {
            if (A[i] != 0) {
                System.out.println(i + ":" + A[i]);
            }
        }
    }
}

第十一章散列查找

1 电话聊天狂人

给定大量手机用户通话记录，找出其中通话次数最多的聊天狂人。

输入格式:
输入首先给出正整数N（≤10⁵），为通话记录条数。随后N行，每行给出一条通话记录。简单起见，这里只列出拨出方和接收方的11位数字构成的手机号码，其中以空格分隔。
输入样例：

4
13005711862 13588625832
13505711862 13088625832
13588625832 18087925832
15005713862 13588625832

输出格式:
在一行中给出聊天狂人的手机号码及其通话次数，其间以空格分隔。如果这样的人不唯一，则输出狂人中最小的号码及其通话次数，并且附加给出并列狂人的人数。
输出样例：

1	13588625832 3

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Map<String, Integer> phoneNumber = new HashMap<String, Integer>();
        Scanner scan = new Scanner(System.in);
        int N = scan.nextInt();
        for (int i = 0; i < 2 * N; i++) {
            String n = scan.next();
            if (phoneNumber.containsKey(n)) {
                phoneNumber.put(n, phoneNumber.get(n) + 1);
            } else {
                phoneNumber.put(n, 1);
            }
        }
        int max = 0, value = 0;
        List<String> number=new ArrayList<>();
        String Num = "99999999999";
        for (String key:phoneNumber.keySet()){
            value = phoneNumber.get(key);
            if(max < value){
                max = value;
            }
        }
        for (String key:phoneNumber.keySet()){
            if(phoneNumber.get(key) == max){
                number.add(key);
            }
        }

        if (number.size() == 1) {
            System.out.println(number.get(0) + " " + max);
        } else {
            for (String key : number) {
                if (key.compareTo(Num) < 0) {
                    Num = key;
                }
            }
            System.out.println(Num + " " + max + " " + number.size());
        }


    }
}

2 QQ帐户的申请与登陆

实现QQ新帐户申请和老帐户登陆的简化版功能。最大挑战是：据说现在的QQ号码已经有10位数了。

输入格式:
输入首先给出正整数N（≤10⁵），随后给出N行指令。每行指令的格式为：“命令符（空格）QQ号码（空格）密码”。其中命令符为“N”（代表New）时表示要新申请一个QQ号，后面是新帐户的号码和密码；命令符为“L”（代表Login）时表示是老帐户登陆，后面是登陆信息。QQ号码为一个不超过10位、但大于1000（据说QQ老总的号码是1001）的整数。密码为不小于6位、不超过16位、且不包含空格的字符串。
输入样例：

5
L 1234567890 myQQ@qq.com
N 1234567890 myQQ@qq.com
N 1234567890 myQQ@qq.com
L 1234567890 myQQ@qq
L 1234567890 myQQ@qq.com

输出格式:
针对每条指令，给出相应的信息：
1）若新申请帐户成功，则输出“New: OK”；
2）若新申请的号码已经存在，则输出“ERROR: Exist”；
3）若老帐户登陆成功，则输出“Login: OK”；
4）若老帐户QQ号码不存在，则输出“ERROR: Not Exist”；
5）若老帐户密码错误，则输出“ERROR: Wrong PW”。
输出样例：

ERROR: Not Exist
New: OK
ERROR: Exist
ERROR: Wrong PW
Login: OK

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Map<String, String> QQNumber = new HashMap<String, String>();
        Scanner scan = new Scanner(System.in);
        int N = scan.nextInt();
        for (int i = 0; i < N; i++) {
            String order = scan.next();
            String number = scan.next();
            String password = scan.next();
            if (Objects.equals(order, "N")) {
                if (QQNumber.containsKey(number)) {
                    System.out.println("ERROR: Exist");
                } else {
                    QQNumber.put(number, password);
                    System.out.println("New: OK");
                }

            } else {
                if (QQNumber.containsKey(number)) {
                    if (!Objects.equals(QQNumber.get(number), password)) {
                        System.out.println("ERROR: Wrong PW");
                    } else {
                        System.out.println("Login: OK");
                    }
                } else {
                    System.out.println("ERROR: Not Exist");
                }
            }
        }
    }
}

第一章 绪论

1 最大子列和问题

2 最大子列和问题

第二章 线性结构

1 一元多项式的乘法与加法运算

2 两个有序链表序列的合并

3 Pop Sequence

第三章 树结构（上）

1 树的同构

2 List Leaves

第四章 树（中）

1 是否同一棵二叉搜索树

第五章 树（下）

1 堆中的路径

第六章 图（上）

1 列出连通集

2 六度空间

第九章 排序(上)

1 排序

第十章 排序(下)

1 统计工龄

第十一章 散列查找

1 电话聊天狂人

2 QQ帐户的申请与登陆

我们一起来让这个世界有趣一点

第一章绪论

第二章线性结构

第三章树结构（上）

第四章树（中）

第五章树（下）

第六章图（上）

第九章排序(上)

第十章排序(下)

第十一章散列查找