排序算法

1 O(n)2

1
2
3
4
5
6
7
8
9
for(int i = 0 ; i < n ; i ++){
    // 寻找[i, n)区间里的最小值
    int minIndex = i;
    for( int j = i + 1 ; j < n ; j ++ )
        if( arr[j] < arr[minIndex] )
            minIndex = j;

    swap( arr[i] , arr[minIndex] );
}

2 插入排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
for( int i = 1 ; i < n ; i ++ ) {
    
     // 寻找元素arr[i]合适的插入位置
     // 写法1
     for( int j = i ; j > 0 ; j-- )
         if( arr[j] < arr[j-1] )
             swap( arr[j] , arr[j-1] );
         else
             break;
    
     // 写法2
     for( int j = i ; j > 0 && arr[j] < arr[j-1] ; j -- )
         swap( arr[j] , arr[j-1] );
}

3 插入排序优化

swap交换需要赋值三次，可以改进。

1
2
3
4
5
6
7
for(int i = 0 ; i < n ; i ++){
    T e = arr[i];
    int j; // j保存元素e应该插入的位置
    for (j = i; j > 0 && arr[j-1] > e; j--)
        arr[j] = arr[j-1];
    arr[j] = e;
}

4 冒泡排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
bool swapped;

    do{
        swapped = false;
        for( int i = 1 ; i < n ; i ++ )
            if( arr[i-1] > arr[i] ){
                swap( arr[i-1] , arr[i] );
                swapped = true;

            }

        // 优化, 每一趟Bubble Sort都将最大的元素放在了最后的位置
        // 所以下一次排序, 最后的元素可以不再考虑
        n --;

    }while(swapped);

5 希尔排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 计算 increment sequence: 1, 4, 13, 40, 121, 364, 1093...
    int h = 1;
    while( h < n/3 )
        h = 3 * h + 1;

    while( h >= 1 ){

        // h-sort the array
        for( int i = h ; i < n ; i ++ ){

            // 对 arr[i], arr[i-h], arr[i-2*h], arr[i-3*h]... 使用插入排序
            T e = arr[i];
            int j;
            for( j = i ; j >= h && e < arr[j-h] ; j -= h )
                arr[j] = arr[j-h];
            arr[j] = e;
        }

        h /= 3;
    }

6 归并排序

数组分成两半进行排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
void __merge(T arr[], int l, int mid, int r){

    //* VS不支持动态长度数组, 即不能使用 T aux[r-l+1]的方式申请aux的空间
    //* 使用VS的同学, 请使用new的方式申请aux空间
    //* 使用new申请空间, 不要忘了在__merge函数的最后, delete掉申请的空间:)
    T aux[r-l+1];
    //T *aux = new T[r-l+1];

    for( int i = l ; i <= r; i ++ )
        aux[i-l] = arr[i];

    // 初始化，i指向左半部分的起始索引位置l；j指向右半部分起始索引位置mid+1
    int i = l, j = mid+1;
    for( int k = l ; k <= r; k ++ ){

        if( i > mid ){  // 如果左半部分元素已经全部处理完毕
            arr[k] = aux[j-l]; j ++;
        }
        else if( j > r ){  // 如果右半部分元素已经全部处理完毕
            arr[k] = aux[i-l]; i ++;
        }
        else if( aux[i-l] < aux[j-l] ) {  // 左半部分所指元素 < 右半部分所指元素
            arr[k] = aux[i-l]; i ++;
        }
        else{  // 左半部分所指元素 >= 右半部分所指元素
            arr[k] = aux[j-l]; j ++;
        }
    }

    //delete[] aux;
}

// 递归使用归并排序,对arr[l...r]的范围进行排序
template<typename T>
void __mergeSort(T arr[], int l, int r){
    //判断数组合法性
    if( l >= r )
        return;

    int mid = (l+r)/2;
    __mergeSort(arr, l, mid);
    __mergeSort(arr, mid+1, r);
    __merge(arr, l, mid, r);
}

template<typename T>
void mergeSort(T arr[], int n){

    __mergeSort( arr , 0 , n-1 );
}

7 归并排序优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
template<typename T>
void __mergeSort2(T arr[], int l, int r){

    // 优化2: 对于小规模数组, 使用插入排序
    if( r - l <= 15 ){
        insertionSort(arr, l, r);
        return;
    }

    int mid = (l+r)/2;
    __mergeSort2(arr, l, mid);
    __mergeSort2(arr, mid+1, r);

    // 优化1: 对于arr[mid] <= arr[mid+1]的情况,即完全有序，不进行merge
    // 对于近乎有序的数组非常有效,但是对于一般情况,有一定的性能损失
    if( arr[mid] > arr[mid+1] )
        __merge(arr, l, mid, r);
}

template<typename T>
void mergeSort2(T arr[], int n){

    __mergeSort2( arr , 0 , n-1 );
}

8 自底向上归并排序

变递归为迭代，而且可用于链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
template <typename T>
void mergeSortBU(T arr[], int n){

// Merge Sort Bottom Up 无优化版本
    for( int sz = 1; sz < n ; sz += sz )
        //保证i+sz<n
        for( int i = 0 ; i < n - sz ; i += sz+sz )
            // 对 arr[i...i+sz-1] 和 arr[i+sz...i+2*sz-1] 进行归并
            __merge(arr, i, i+sz-1, min(i+sz+sz-1,n-1) );


    // Merge Sort Bottom Up 优化
    // 对于小数组, 使用插入排序优化
    for( int i = 0 ; i < n ; i += 16 )
        insertionSort(arr,i,min(i+15,n-1));

    for( int sz = 16; sz < n ; sz += sz )
        for( int i = 0 ; i < n - sz ; i += sz+sz )
            // 对于arr[mid] <= arr[mid+1]的情况,不进行merge
            if( arr[i+sz-1] > arr[i+sz] )
                __merge(arr, i, i+sz-1, min(i+sz+sz-1,n-1) );

    // Merge Sort BU 也是一个O(nlogn)复杂度的算法，虽然只使用两重for循环
    // 所以，Merge Sort BU也可以在1秒之内轻松处理100万数量级的数据
    // 注意：不要轻易根据循环层数来判断算法的复杂度，Merge Sort BU就是一个反例

}


// 比较Merge Sort和Merge Sort Bottom Up两种排序算法的性能效率
// 整体而言, 两种算法的效率是差不多的。但是如果进行仔细测试, 自底向上的归并排序会略胜一筹。

9 快速排序

将第一个元素作为标记点，找到该标记的正确位置，之前的元素小于标记元素，之后的元素大于标记元素。

快速排序

快速排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
int __partition(T arr[], int l, int r){

    T v = arr[l];

    int j = l; // arr[l+1...j] < v ; arr[j+1...i) > v
    for( int i = l + 1 ; i <= r ; i ++ )
        if( arr[i] < v ){
            j ++;
            swap( arr[j] , arr[i] );
        }
    //最后将v放入正确位置
    swap( arr[l] , arr[j]);

    return j;
}

// 对arr[l...r]部分进行快速排序
template <typename T>
void __quickSort(T arr[], int l, int r){

    if( l >= r )
        return;

    int p = __partition(arr, l, r);
    __quickSort(arr, l, p-1 );
    __quickSort(arr, p+1, r);
}

template <typename T>
void quickSort(T arr[], int n){

    __quickSort(arr, 0, n-1);
}


// 比较Merge Sort和Quick Sort两种排序算法的性能效率
// 两种排序算法虽然都是O(nlogn)级别的, 但是Quick Sort算法有常数级的优势
// Quick Sort要比Merge Sort快, 即使我们对Merge Sort进行了优化

10 随机化快速排序

随机选择标定点，改善近似顺序列表排序性能

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
// 对arr[l...r]部分进行partition操作
// 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
template <typename T>
int _partition(T arr[], int l, int r){

    // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
    swap( arr[l] , arr[rand()%(r-l+1)+l] );

    T v = arr[l];
    int j = l;
    for( int i = l + 1 ; i <= r ; i ++ )
        if( arr[i] < v ){
            j ++;
            swap( arr[j] , arr[i] );
        }

    swap( arr[l] , arr[j]);

    return j;
}

// 对arr[l...r]部分进行快速排序
template <typename T>
void _quickSort(T arr[], int l, int r){

    // 对于小规模数组, 使用插入排序进行优化
    if( r - l <= 15 ){
        insertionSort(arr,l,r);
        return;
    }

    int p = _partition(arr, l, r);
    _quickSort(arr, l, p-1 );
    _quickSort(arr, p+1, r);
}

template <typename T>
void quickSort(T arr[], int n){

    srand(time(NULL));
    _quickSort(arr, 0, n-1);
}

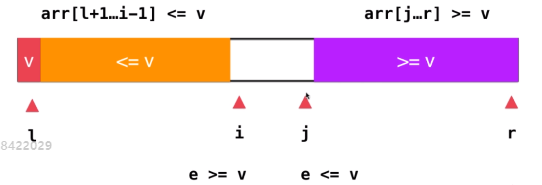
11 双路快速排序

从两头向中间执行partition，使等于v的元素分散在两边，使两部分尽量平衡，适用于大量重复数据的场合

双路快速排序

双路快速排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
// 双路快速排序的partition
// 返回p, 使得arr[l...p-1] <= arr[p] ; arr[p+1...r] >= arr[p]
// 双路快排处理的元素正好等于arr[p]的时候要注意，详见下面的注释：）
template <typename T>
int _partition2(T arr[], int l, int r){

    // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
    swap( arr[l] , arr[rand()%(r-l+1)+l] );
    T v = arr[l];

    // arr[l+1...i) <= v; arr(j...r] >= v
    int i = l+1, j = r;
    while( true ){
        // 注意这里的边界, arr[i] < v, 不能是arr[i] <= v
        while( i <= r && arr[i] < v )
            i ++;

        // 注意这里的边界, arr[j] > v, 不能是arr[j] >= v
        while( j >= l+1 && arr[j] > v )
            j --;

        // 多了个等号的判断会造成两棵子树不平衡

        if( i > j )
            break;

        swap( arr[i] , arr[j] );
        i ++;
        j --;
    }

    swap( arr[l] , arr[j]);

    return j;
}

// 对arr[l...r]部分进行快速排序
template <typename T>
void _quickSort(T arr[], int l, int r){

    // 对于小规模数组, 使用插入排序进行优化
    if( r - l <= 15 ){
        insertionSort(arr,l,r);
        return;
    }

    // 调用双路快速排序的partition
    int p = _partition2(arr, l, r);
    _quickSort(arr, l, p-1 );
    _quickSort(arr, p+1, r);
}

template <typename T>
void quickSort(T arr[], int n){

    srand(time(NULL));
    _quickSort(arr, 0, n-1);
}

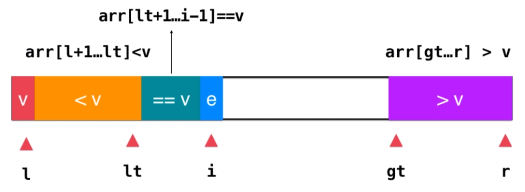
12 三路快速排序

三路快速排序

三路快速排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
// 递归的三路快速排序算法
template <typename T>
void __quickSort3Ways(T arr[], int l, int r){

    // 对于小规模数组, 使用插入排序进行优化
    if( r - l <= 15 ){
        insertionSort(arr,l,r);
        return;
    }

    // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
    swap( arr[l], arr[rand()%(r-l+1)+l ] );

    T v = arr[l];

    int lt = l;     // arr[l+1...lt] < v
    int gt = r + 1; // arr[gt...r] > v
    int i = l+1;    // arr[lt+1...i) == v
    while( i < gt ){
        if( arr[i] < v ){
            swap( arr[i], arr[lt+1]);
            i ++;
            lt ++;
        }
        else if( arr[i] > v ){
            swap( arr[i], arr[gt-1]);
            gt --;
        }
        else{ // arr[i] == v
            i ++;
        }
    }

    swap( arr[l] , arr[lt] );

    __quickSort3Ways(arr, l, lt-1);
    __quickSort3Ways(arr, gt, r);
}

template <typename T>
void quickSort3Ways(T arr[], int n){

    srand(time(NULL));
    __quickSort3Ways( arr, 0, n-1);
}


// 比较Merge Sort和双路快速排序和三路快排三种排序算法的性能效率
// 对于包含有大量重复数据的数组, 三路快排有巨大的优势
// 对于一般性的随机数组和近乎有序的数组, 三路快排的效率虽然不是最优的, 但是是在非常可以接受的范围里
// 因此, 在一些语言中, 三路快排是默认的语言库函数中使用的排序算法。比如Java:)